Zobrazování figurek v letadle (definice)

2024 Autor: Leah Sherlock | [email protected]. Naposledy změněno: 2023-12-17 05:30

Schopnost správně zobrazit různé tvary na rovině listu, plátna a jakéhokoli jiného povrchu je poměrně významná dovednost. A především je to důležité jak pro umělce: malíře, sochaře, grafiky, designéry (vnitřních prostorů a architektonického prostředí), tak pro vědce: matematiky, fyziky, designéry, vynálezce.

Je ale také důležité, aby se člověk, který je vzdálen od těchto sfér, naučil správně vnímat a zobrazovat svět kolem sebe. To pomáhá mnohem hlouběji porozumět celé jeho všestrannosti. Pokud nemáte dostatečnou představu o tom, jak to správně udělat, pak s velkou pravděpodobností neuspějete s projektem, obrázkem nebo kresbou žádného vynálezu. To znamená, že tato dovednost je důležitá jak pro řešení jednoduchých, každodenních úkolů, tak pro ty, které mají globální, univerzální význam.

Trocha historie

Od pradávna se lidé snažili znázornit to, co viděli kolem sebe: ostatní lidi, nějaké primitivní stavby té doby, úžasně krásný svět rostlin a zvířat, majestátní hory a prostě věci, věci do domácnosti. Tedy svět v celé jeho rozmanitosti a vznešenosti.

To ale ještě netušili, jak by se to dalo udělat přesně a kompetentně, aby zobrazení různých trojrozměrných objektů v rovině bylo opravdu realistické, živé. Ten člověk neměl příslušné znalosti a navíc neměl žádné speciální dovednosti, snad kromě těch nejzákladnějších.

V dřívějších zdrojích se uvádí, že první obraz na světě sestával pouze z jedné linie, která vedla podél stínu člověka vrženého sluncem na zeď. To znamená, že příroda sama navrhla, kterým směrem se vyplatí jít při hledání správného řešení tohoto problému.

A tato otázka znepokojovala tehdejšího muže i z tohoto důvodu: nechtěl jen obdivovat objemnou živou siluetu, takříkajíc originál, ale snažil se zachytit prostorový objekt na rovině. A udělal to proto, aby si tímto způsobem mohl buď vyzdobit svůj domov nebo místo pro něj posvátné, nebo si s sebou vzít balíček s obrázkem a přesunout jej na libovolnou vzdálenost.

Geometrie vzoru

A co říkáte, ale ubíhaly roky, ubíhala staletí a jak se civilizace vyvíjela, lidé se postupně naučili zobrazovat složité postavy ve dvourozměrném prostoru, tedy v rovině. Teprve nyní se přesnost velikostí a proporcí zobrazených objektů začala zdát velmi přibližná.

Otázka, jak správně je zobrazení postavy v rovině a do jaké míry odpovídají objemu původních objektů, se však kdysi stala velmi aktuální. Nějakým způsobem nová věda tzvgeometrie. Přesněji řečeno, jeho část je deskriptivní geometrie.

Zde jen studuje tvary a roviny, čáry a body, stejně jako jejich vzájemný vztah – v trojrozměrném i dvourozměrném prostoru.

Metody konverze

Důležitým prvkem ve výtvarném umění je zobrazování postav v rovině obrazu. Ostatně ve skutečnosti jde o zachycení trojrozměrných prostorových objektů ve dvourozměrnosti. Totiž: komplex musí být převeden na jednoduchý, to znamená, že objekt, který má délku, šířku, výšku, musí být přenesen do roviny.

A deskriptivní geometrie takové „přechody“díky některým metodám dělá. Celkem jich je asi šest. Zde jsou tři hlavní a nejoblíbenější po celém světě:

• perspektiva (když je zobrazený objekt odstraněn v prostoru);
• ortogonální projekce (projekce rovnoběžná, kde jsou paprsky kolmé k rovině);
• šikmé promítání (projekce rovnoběžná, kde jsou paprsky nakloněny vzhledem k rovině).

Zobrazený objekt se v axonometrické projekci (která zahrnuje ortogonální a šikmou) jeví zcela jasně. Ale nejjasněji a nejpravdivěji se promítá, když je zobrazen v perspektivě. A právě výše uvedené metody do značné míry řeší otázku, jak zobrazit postavy v rovině.

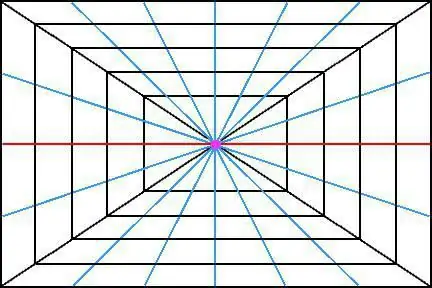
Perspektiva

Perspektiva zaujímá mezi ostatními metodami zobrazení nejčestnější místo. Protože lidské okopodobně jako čočka fotoaparátu vidí okolní prostor podobným způsobem. Věci, které jsou dále od pozorovatele, se zdají menší a někdy mnohem menší, než když jsou blízko.

Udělejte si například obrázek krychle v prostoru. Pokud jsou ve skutečnosti všechny jeho hrany vzájemně rovnoběžné, pak se při pohledu na tento objekt v dálce může zdát, že se hrany sbíhají (nebo by měly sbíhat) v jednom bodě. A co je nejzajímavější, neměly by se pouze sbíhat v jednom bodě, ale měly by mít jeden průsečík.

Díky mistrům renesance: Albrechtu Dürerovi, Piero Della Francesca, Andrea Mantegna, Leon Batista Alberti moderní malba ví, co je přímá lineární perspektiva, jak určit výšku horizontu a úběžníky.

A světově proslulý génius - Leonardo da Vinci - poprvé argumentoval konceptem letecké perspektivy. To zahrnuje změnu barvy, tónu objektu, změny jeho kontrastních charakteristik (klesající, jak se objekt vzdaluje).

Ortografická projekce

Ortogonální se nazývá rovnoběžné promítání, které směřuje k přímce, která je kolmá k rovině. V procesu jeho aplikace zůstávají rozměry obrysů objektu nezměněny. To znamená, že objekt je zobrazen bez zkreslení.

Promítaný trojrozměrný objekt je jakoby rozložen do tří pohledů: ze strany, zepředu a shora. A když se na to všechno zároveň podíváte, můžete přidatreprezentace toho, jak objekt vypadá v objemu. Rozměry figury přitom zůstávají nezměněny jak v trojrozměrném, tak ve dvourozměrném obrazu.

Šikmá projekce

Tato projekce je rozdělena do několika dalších poddruhů, konkrétně:

• izometrický pohled;
• dimetrická projekce;
• trimetrická projekce.

Izometrický má koeficienty zkreslení ve všech 3 osách (délka, šířka, výška). To znamená, že úhly mezi osami odebranými v párech jsou rovné 120 stupňům. V dimetrickém jsou zkreslení podél 2 os stejné a třetí je odlišné. A v trimetrické projekci jsou všechny koeficienty zkreslení (tj. podél všech 3 os) různé.

Tvary rotace

Když se pravoúhlý trojúhelník otáčí podél osy jedné ze dvou nohou, jeho třetí strana (hypotenuze) bude popisovat nový útvar zvaný kužel. A pokud otočíte obdélník (čtverec) podél jedné z jeho stran, získáte válec. Když se půlkruh otočí, vyjde koule.

Z toho vyplývá, že otočením roviny podél nějaké osy získáme tzv. čísla rotace.

Tyto postavy mají osu otáčení. To, jak vypadají v rovině, závisí na jejich umístění vzhledem k úrovni očí. Například horní a spodní strana válce jsou v podstatě kruhy. A když se na ně podíváte v letadle, vypadají jako elipsy.

Úkol se však stává ještě obtížnějším, když při zobrazováníprostorové obrazce na rovině, mají nakloněnou osu. V tomto případě je důležité, aby obrysy rotačních těles byly ve stejné vzdálenosti od osy rotačních těles.

Něco málo o šerosvitu

Chiaroscuro hraje důležitou roli při zobrazování obrazců v letadle. Protože objem zobrazovaného předmětu vzniká nejen díky liniím, ale také díky správnému rozložení světla a stínu po jeho stranách. A pak to vypadá docela objemně v rovině dvourozměrného povrchu.

Zobrazování obrazců v rovině, určování jejich velikostí, vlastnosti správného překrytí světlosti a tmavých skvrn je tedy díky výše uvedeným metodám docela možné. A hlavně se jedná o skutečně osvědčené metody v praxi, které používají přední odborníci naší doby.